My self is steam

Insights into computer security, programming and math

May 21, 2020
Timing Attack Side Channel in IAIK JCE DSA Implementation

IAIK-JCE is a provider for the Java Cryptography Extension that, according to the vendor, "supplements the security functionality of the default JDK". It is a commercial product developed by Stiftung Secure Information and Communication Technologies, a spin-off of the Institute for Applied Information Processing and Communication” (IAIK) of the University of Graz. The company is kind enough to offer a full, free evaluation version for any non-commercial use.

By observing the behavior of the latest version (5.60 as of today), one can get a glimpse of how the major cryptographic algorithms are implemented. This process led me to the discovery of a subtle vulnerability in the implementation of the DSA algorithm: the way that some of the computations involved in the signature generation are carried out introduces a side channel that leaks timing information from the observation of which an attacker could potentially recover the private key.

The same kind of issue affected other popular JCE providers, for instance CVE-2016-5548, CVE-2016-1000341, CVE-2019-3739, and it's related to the fact that a flawed implementation typically relies on non-constant-time modular exponentiation to compute parts of the signature. Let's quickly review how signatures are generated in the general setting of the DSA algorithm. Let Zp* be the reduced residue system modulo a prime p whose length is usually chosen among 1024, 2048, 3072, 4096. This set forms a cyclic group of cardinality φ(p)=p-1 under multiplication. A consequence of Lagrange's theorem is that we can construct a cyclic subgroup of Zp* with cardinality equal to a smaller prime q by choosing p so that q divides p-1. Since the order of any element of Zp* must divide p-1, by choosing a random a ≤ p-1 we obtain a primitive element that generates the whole subgroup of order q by g=ap-1q. This makes the subgroup closed under multiplication modulo p and, by consequence, under exponentiation, so that any power of g still belongs to the subgroup. We will call y=gx the public key whereas a randomly chosen x≤q-1 is the private key.

Given a message m, a signature is the couple (r,s), generated as follows:

r=(gk mod p) mod q
s=(k-1(H(m)+xr)) mod q

Where 1≤k≤q-1 is randomly chosen and H denotes a hash function whose digest length matches the length of q. The modular exponentiation of big integers is usually implemented by means of a technique named exponentiation by squaring, which exploits the binary representation of the exponent to perform fast computations compared to the trivial iterated-multiplication. The observable running time is therefore a function dependent on either the length or the binary representation of the exponent. As it turns out, this is enough to introduce a time correlation between the exponent and the computation of the result, and an attacker who carefully observes the time taken to generate the signatures could extract partial information about the exponent k. This partial information could be used to recover the whole exponent and therefore the private key x, as there exist techniques to reconstruct an integer of a prime field like Zp* knowing only a few bits of it. This kind of side channels is usually thwarted in software implementations with the help of a technique named blinding, where a further random integer is multiplied with the exponent before the exponentiation. Another mitigation option is the Montgomery's ladder.

Enough of an introduction. Let's see how the IAIK JCE provider implements the DSA algorithm. RawDSA.class has the symbol names stripped so we have to understand which dummy symbol maps to the right DSA parameter. This is easily accomplished by gathering the following lines from across the code: 

  protected void engineInitVerify(PublicKey paramPublicKey) throws InvalidKeyException {
...
    this.b = dSAPublicKey.getY();
...
  protected void engineInitSign(PrivateKey paramPrivateKey) throws InvalidKeyException {
...
    this.a = dSAPrivateKey.getX();
...
  private void a(DSAParams paramDSAParams) {
    this.c = paramDSAParams.getP();
    this.d = paramDSAParams.getQ();
    this.e = paramDSAParams.getG();
  }

We are then able to identify all the parameters: 

public final class RawDSA extends SignatureSpi {
  private BigInteger a;     // <--- x, private key
  
  private BigInteger b;     // <--- y = g^x, public key
  
  private BigInteger c;     // <--- p
  
  private BigInteger d;     // <--- q
  
  private BigInteger e;     // <--- g
...

Let's now focus on the signature generation. 

  public BigInteger[] dsaSignRS() {
    byte[] arrayOfByte = this.dataBuffer_.toByteArray();
    if (this.i != null)
      this.i.a(this.a, arrayOfByte);
    while (true) {
①      BigInteger bigInteger1 = a();
②      BigInteger bigInteger2 = a(bigInteger1);
      if (bigInteger2.equals(NumberTheory.ZERO))
        continue;
      BigInteger bigInteger3 = a(bigInteger1, bigInteger2, arrayOfByte);
      if (!bigInteger3.equals(NumberTheory.ZERO))
        return new BigInteger[] { bigInteger2, bigInteger3 };
    }
  }

The two bigInteger of interest are all returned by a method `a` having three different signatures. The first takes no formal parameters: 

① private BigInteger a() {
    BigInteger bigInteger;
    if (this.i != null) {
      bigInteger = this.i.a();
    } else {
      BigInteger bigInteger1;
      if (this.g == null) {
        if (this.f == null)
          this.f = SecRandom.getDefault();
        int i = this.d.bitLength() + 64;
        bigInteger1 = new BigInteger(i, this.f);
      } else {
        bigInteger1 = new BigInteger(1, this.g);
        bigInteger1 = bigInteger1.subtract(NumberTheory.ONE);
      }
      bigInteger = bigInteger1.mod(this.d.subtract(NumberTheory.ONE)).add(NumberTheory.ONE);
    }
    return bigInteger;
  }

The code above combines the two algorithms that generate the unique ephemeral number k, as described in the NIST FIPS 186-4 document, appendices B.2.1 and B.2.2, according to which a c obtained from the RBG is then returned as: k=(c mod (q-1))+1.

Let's find out what line ② does. The method returns a BigInteger and takes the ephemeral k as argument; this is indeed the method that calculates r: 

② private BigInteger a(BigInteger paramBigInteger) {
    BigInteger bigInteger = this.e.modPow(paramBigInteger, this.c);
    return bigInteger.mod(this.d);
  }

This is where the modular exponentiation is performed. The code uses Java BigInteger's modPow, whose underlying algorithm uses a variant of the Sliding-window method, itself a form of exponentiation-by-squaring: the exponent is decomposed into two parts that are then discriminated according to whether they are even or odd. The former part leads to a completely different set of operations than the latter, introducing then the dependency on the input. This is what makes the IAIK DSA implementation vulnerable to the timing attack.

We want to verify our claim with the help of a proof of concept: if it's true that the code is vulnerable, a certain correlation between either r or the ephemeral k generated at ①, and the time taken to compute the signature must arise. We therefore generate a large number of signatures and measure the time taken by each signature, and record it along with the value of each signature's r and k. The code for the PoC is available here. An entropy daemon like Haveged is recommended or, at the very least, java.security.egd must point to /dev/urandom, since most Java implementations use /dev/random by default and the code could therefore block, waiting for more entropy to be harvested. The output from the program looks like: 

time;r;k
3040211;304545110037792108352155616342187874653439775526;792415407494206255999175588330041765090379724621
1759846;994456083602324492753775613997634890006734890312;1147064693348440745986375215220663950617549464466
1567922;1100375385524368117595997104661333932876798141866;526303025493376784355601406592090222158889264898
...

We test our hypothesis of a dependency between the time and any of r or k by calculating the Spearman's correlation coefficient between the three variables in the dataset. This choice is justified by the fact that we make no assumption on the linearity of the correlation, the only hypothesis being that, intuitively, the time must be monotonically related with one of the two variables, since larger exponents would imply longer times for the exponentiation. The correlation coefficients that I obtained for a dataset of 100000 signatures are: 

          time         r         k
time  1.000000 -0.005567  0.226051
r    -0.005567  1.000000 -0.006712
k     0.226051 -0.006712  1.000000

The variable r shows no correlation with the time, as the coefficient is practically zero, while, unsurpinsingly, the variable k shows a positive correlation coefficient of 0.226, confirming the monotonical relation with the values of the time. This can be also seen from the scatter plot with the time variable on the vertical axis, and k on the horizontal:

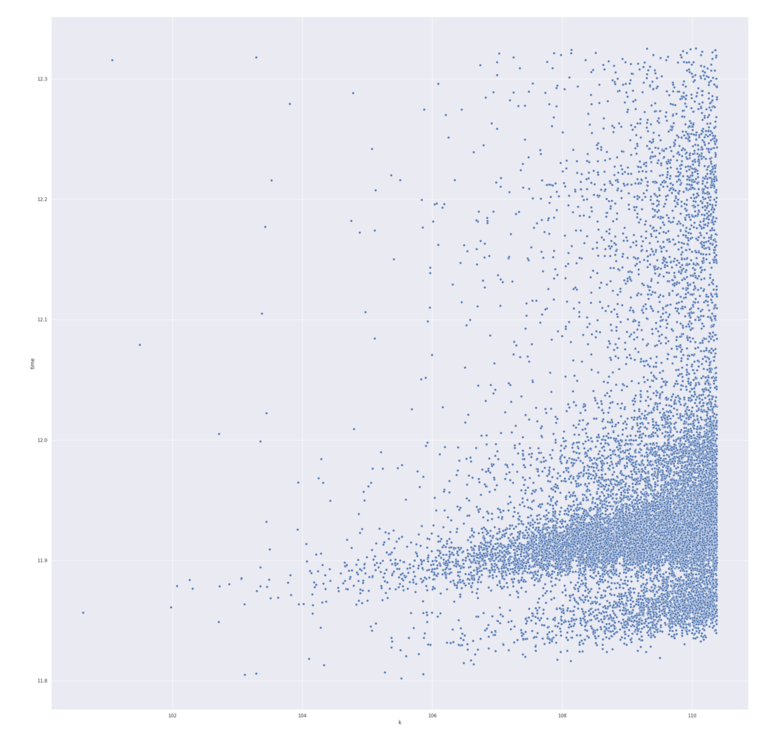
One might argue over the small value of the correlation coefficient. We provide an experimental counter argument to convince ourselves of the quality of the test. We generate similar datasets with the exactly the same code of the PoC against two different Java JCE providers: BouncyCastle version 1.54 and 1.64, respectively. BouncyCastle versions earlier than 1.56 are all affected by a similar vulnerability. We compute the Spearman's coefficient for each dataset produced by timing the signatures generated with each version. The values obtained for version 1.64, which is "immune" due to blinding, are: 

          time         r         k
time  1.000000  0.001817  0.002297
r     0.001817  1.000000 -0.008206
k     0.002297 -0.008206  1.000000

Indeed, the blinding technique eliminates any sort of monotonical correlation between k and the time. Let's compare that to the coefficients obtained for version 1.54, vulnerable as per CVE-2016-1000341: 

          time         r         k
time  1.000000 -0.005543  0.204165
r    -0.005543  1.000000 -0.006380
k     0.204165 -0.006380  1.000000

We clearly see the coefficient of the correlation between k and the time to be roughly the same value as the one we obtained for the IAIK JCE provider. This completes the discussion by adding more evidence to our former claim regarding the vulnerability, and a reasonably good confidence on the effectiveness of our testing technique.